Kraftstoß schief | Eisschießen

Kraftstoß

Der schiefe, zentrale Stoß

Bei einem versetzten (schiefen) Stoß liegen die nicht die Geschwindigkeitsvektoren der Stoßpartner nicht auf der → Stoßnormalen. Fallen ggf. unter Vernachlässigung der Reibung an den Berührungsflächen Stoßnormale und → Stoßlinie zusammen, so spricht man von einem versetzten, zentralen Stoß.

Die Größe des Kraftstoßes wird durch die Massen der Stoßkörper, die Aufprallgeschwindigkeit, die → Rückprallelastizität und zusätzlich durch den Aufprallwinkel ∝ bestimmt.

– nach oben –

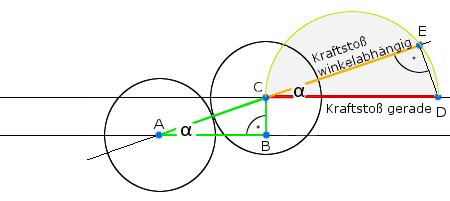
Der Aufprallwinkel

Im Dreieck ABC entspricht die Strecke AC der Summe aus den Radien der Stoßkörper (ca. 27 cm) und die Strecke BC dem (senkrechten) Abstand des Schwerpunktes des Stoßkörpers B (Stoßversatz d) zum Geschwindigkeitsvektor (Impulsgeraden) des Stoßkörpers A.

Für cos α bzw. sin α gilt:

$cos\, \alpha = \frac{\sqrt{\overline{ AC}^{2} - (d)^{2}}}{\overline{AC}}$

und

$sin\, \alpha = \frac{(d)}{\overline{AC}}$

onChange=“calcWinkel()“

Die Stoßversetzung um 0 cm beschreibt einen geraden, zentralen Stoß. Bei einer Stoßversetzung um mehr als 27 cm findet kein Kraftstoß statt, es kommt zu keiner Berührung der Stoßkörper.

– nach oben –

Kraftstoß und Winkelfunktion

Bei einem schiefen, zentralen Stoß wirkt der Kraftstoß abhängig vom Aufprallwinkel. Da die Dreiecke ABC und CDE der Darstellung unten ähnlich ¹ sind, ergibt sich unter Vernachlässigung der Reibung an den Berührungsflächen (glatter Stoß) der wirkendende Kraftstoß aus Kraftstoß • cos α.

Größe des Kraftstoßes (S):

$Kraftstoss (S) = \frac{m_{1}\cdot m_{2}\cdot v_{1}(1+k)}{m_{1}+m_{2}} \cdot {\color{Red} \mathbf{\cos\alpha}}$

Geschwindigkeit Stoßkörper 2 (v₂) nach Stoß:

$v_{2}{}'=&space;\frac{m_{1}\cdot&space;v_{1}(1-k)}{m_{1}+m_{2}} \cdot {\color{Red} \cos \alpha }$

– nach oben –

Verformungsarbeit

Die durch bleibende Verformungen und innere Reibung in Wärme umgewandelte innere Energie erhält man durch Anwendung von (cos α)² auf die Werte beim geraden Stoß.

Verformungsarbeit (W):

$W = \frac{m_{1}\cdot m_{2}}{2 (m_{1}+m_{2})}\cdot v_{1}{}^{2}\cdot (1-k^{2}) \cdot {\color{Red} \cos \alpha ^{2}}$

– nach oben –

Rückstoß und resultierender Vektor

Nach 1. Newtonsches Axiomdem (Wechselwirkungsgesetz) erhält der Stoßkörper 1 beim Kraftstoß einen Rückstoß in gleicher Höhe. Durch Vektoraddition (ursprünglicher Impuls und Rückstoß) erhält man als Ergebnis (resultierender Vektor) den Impuls des Stoßkörpers 1 nach dem Kraftstoß.

– nach oben –

(h) = Kraftstoß • sin α:

$(h) = \frac{m_{1}\cdot m_{2}\cdot v_{1}\cdot (1-k)\cdot {\color{Red} \cos \alpha} \cdot {\color{Red} \sin \alpha} }{m_{1}+m_{2}}$

(z) = Impuls – Kraftstoß • cos α:

$(z) = m_{1} \cdot v^{_1} - \frac{m_{1}\cdot m_{2}\cdot v_{1}\cdot (1-k)\cdot {\color{Red} \cos \alpha} \cdot {\color{Red} \cos \alpha} }{m_{1}+m_{2}}$

Geschwindigkeit Stoßkörper 1 (v₁) nach Stoß:

$v_{1}{}'= \frac{\sqrt{(h)^{2}+(z)^{2}}}{m_{1}}$

Abprallwinkel β:

$\cos \beta = \frac{(z)}{\sqrt{(h)^{2}+(z)^{^{2}}}}$

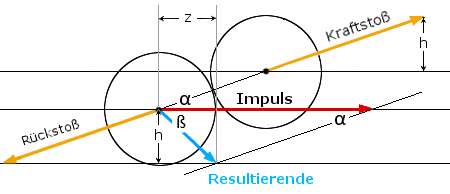Unter Berücksichtigung der Geschwindigkeitsverluste aufgrund des Abstandes der Stoßkörper ergeben sich nachfolgende → Laufwege.

Dreiecke sind „ähnlich“ wenn sie formgleich sind, aber eine unterschiedliche Größe aufweisen. Die Innenwinkel ähnlicher Dreiecke sind gleich. ↩

Strecke AC ≡ r₁ + r₂ = 27.0 cm
Stoßversatz:cm
cos ∝ :
sin ∝ :
Aufprallwinkel ∝ :Grad